
Corollaries
03 July 2018
In mathematical writing a corollary is a result that follows easily from a larger theorem. In particular this result would not be seen as major or difficult but would rather be considered a natural application of a previous theorem. I named this blog Corollaries because that is precisely what I hope to catalog here; neat and short tidbits of mathematics—corollaries.
Corollaries may be small…
But, they can be very cool. For example, the area of a circular ring (an annulus) is found most obviously by subtracting the area of the smaller circle from the area of the larger. This calculation relies however on knowledge of two quantities, but the area of the annulus is actually be determined by only one number [Roher94]. This fact could be considered a corollary to the Pythagorean theorem. Let’s have a quick look at the result.
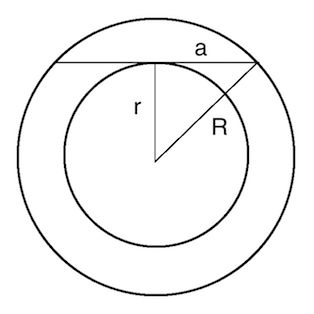
Consider the figure above where \(a\) is half the distance of the chord tangent to the inner circle with \(r\) and \(R\) radii. We want to calculate the area of the annulus in the picture, let’s call it \(A\). Clearly \(A = \pi R^2 - \pi r^2\), the difference of the two circular areas. However, notice that from the right triangle formed by \(a\), \(r\) and \(R\) we also have (by the Pythagorean theorem) \(a^2 + r^2 = R^2\). Multiplying by \(\pi\) we get that
\[\pi a^2 + \pi r^2 = \pi R^2 \\ \pi a^2 = \pi R^2 - \pi r^2 \\ = A.\]Thus the area of the annulus is determined by the distance \(a\) alone and \(A=\pi a^2\). Pretty neat right? I imagine that this fact could find use in some engineering problem where measuring the radii of the circles is impractical or perhaps simplifying some calculation needed to produce a graphic in a computer game. Can you think of any more uses?
Who is this blog for?
I intend to avoid overly complicated proofs in this blog so that anyone with an interest in mathematics can follow the arguments. During a math degree one learns to read and write more and more complicated proofs, a powerful tool of logic, but this is a specialized skill not possessed by everyone. It is my hope that an engineer or computer programmer would find the articles here understandable and entertaining. Hopefully the above corollary sheds some light on the level of mathematics I will be assuming the reader is familiar with.
What to expect.
There are beautiful and surprising results in mathematics that are locked away in textbooks and papers that use so many specialized words and symbols that, even though many people may be interested, only specialists have a hope of understanding these works. I hope to explain in plain language some of my favorite ideas and problems.
- Check out some more cool corollaries to the pythagorean theorem on Cut the Knot.
- [Roher94] D. Rohrer, More Thought Provokers, Key Curriculum Press, 1994